Memory access patterns and performance

Published:

Look, a C function! Take a careful look at what this is doing.

void pagez(int chunks, int iters) {
  #define GIGABYTE 1073741824
  char * allocations[chunks];
  for(int i = 0; i < chunks; i++) {
    allocations[i] = malloc(GIGABYTE);
    assert(allocations[i] != NULL);
  }
  int ps = getpagesize();
  for (int i = 0; i < chunks*iters; i += 1) {
    for (int j = 0; j < GIGABYTE; j += ps)
      allocations[i%chunks][j]++;
  }
  // Skipping free() becuase I like to live on the edge
}

Quick highlights, here’s what this function does:

Now, which of these calls do you think will run faster?

// Option A
pagez(80, 1);
// Option B
pagez(20, 4);

Wait.

Think for a bit.

Don’t cheat and scroll ahead!

Have your answer?

At first glance, you might be tempted to say that they will have the same performance. One of them allocates 80 gigabytes of memory while the other only 20. However, the latter iterates over this memory 4 times, meaning there are the same exact number of memory writes per call. This is a reasonable first stab, but it’s wrong.

You might then take a closer look and pay more attention to the amount of memory being allocated. There’s got to be some overhead to allocating a gigabyte of memory, right? The first program does so 80 times, and the second only 20. Thus, maybe the second program runs faster, because it does not need to allocate as much memory. As it turns out, memory allocation time is basically constant for large chunks like this, so this is also the wrong intuition.

In reality, the second option is slower, by a significant margin:

$ time ./optionA
./optionA  1.02s user 4.80s system 56% cpu 10.228 total
$ time ./optionB
./optionB  1.43s user 8.93s system 73% cpu 14.081 total

This would probably be an even more significant difference if I was running on a machine with slower disk. Alas, this is happening on an M3 Macbook pro, with very fast disk, so there’s “only” a 4 second difference.

Why is this happening? Ultimately it boils down to the memory / disk access pattern, and in turn how the underlying virtual memory system and memory allocation works. So, a little back story.

Virtual Memory

Basically all modern UNIX operating systems use virtual memory, and have for a long time. This means that every process running on the computer is provided with a layer of abstraction that allows it to act as if it is the only program using the entire memory space, while in reality there may be hundreds or thousands of active processes. On top of this, since we have 64 bit processors and memory addresses can be very large, this memory space can be much, much bigger than the physical RAM available on your system. This is why, in the example earlier, I can allocate 80 gigabytes of memory from a single program, even though the computer I tested with only have 16 gigabytes of RAM!

Operating systems have accomplished this abstraction in a variety of ways over the years. In modern systems, the mapping between virtual memory addresses and physical addresses is managed by the OS kernel and the hardware Memory Management Unit.

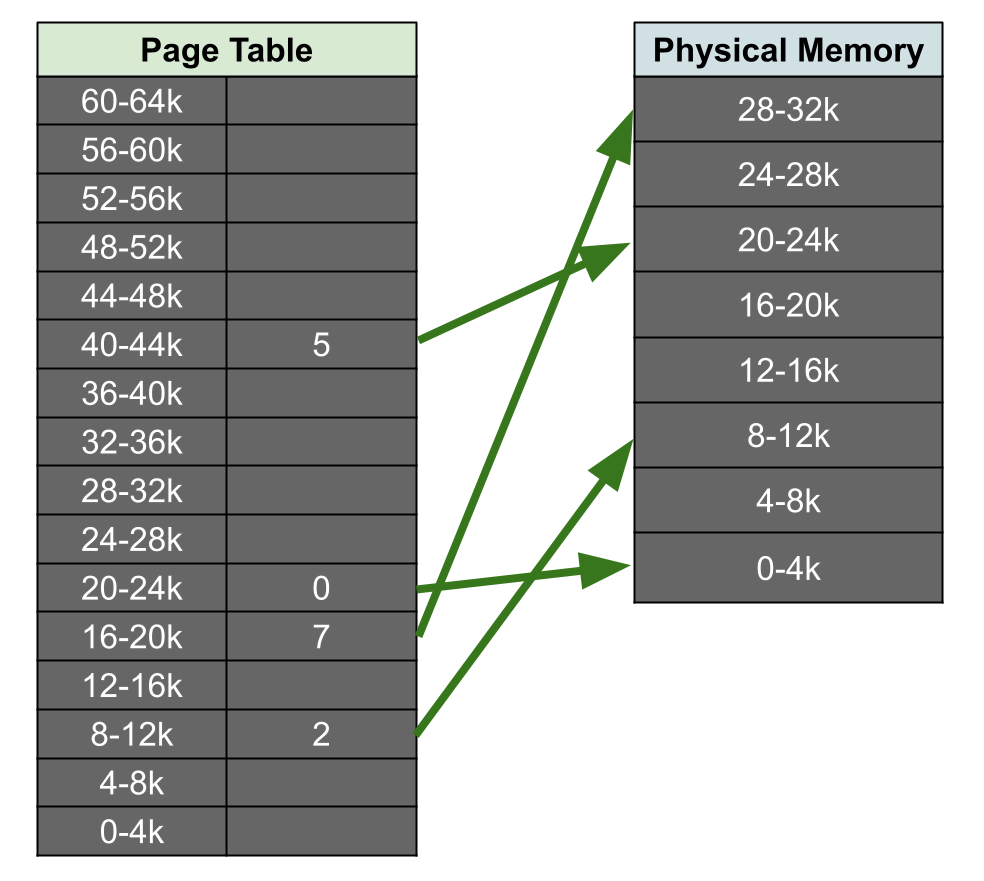
To handle this, the operating system maintains data structure called a page table for each process. A page table is a per-process data structure that contains mappings between the virtual memory pages and physical memory pages. A memory page is a chunk of memory that virtual address spaces are chunked by. The page size is typically something like 4096, 8192, or 16384 bytes. Here’s a little diagram, showing visually what a very small page table might look like, mapping to a very small segment of RAM.

Most modern computers will also have a hardware Memory Management Unit (MMU) that contains a Translation Lookaside Buffer (TLB). The TLB is a cache for the page table. Wow, lots of Three Letter Acronyms (TLAs).

Using memory

A virtual memory address can potentially map to any physical address. Every time memory is needed from RAM by the CPU for instructions running in a userspace process, a translation needs to take place from the virtual address the instruction is using to a physical address in RAM. The exact set of steps for how this is accomplished is (a) complicated and (b) varies between architectures, but a really simplified view looks something like this:

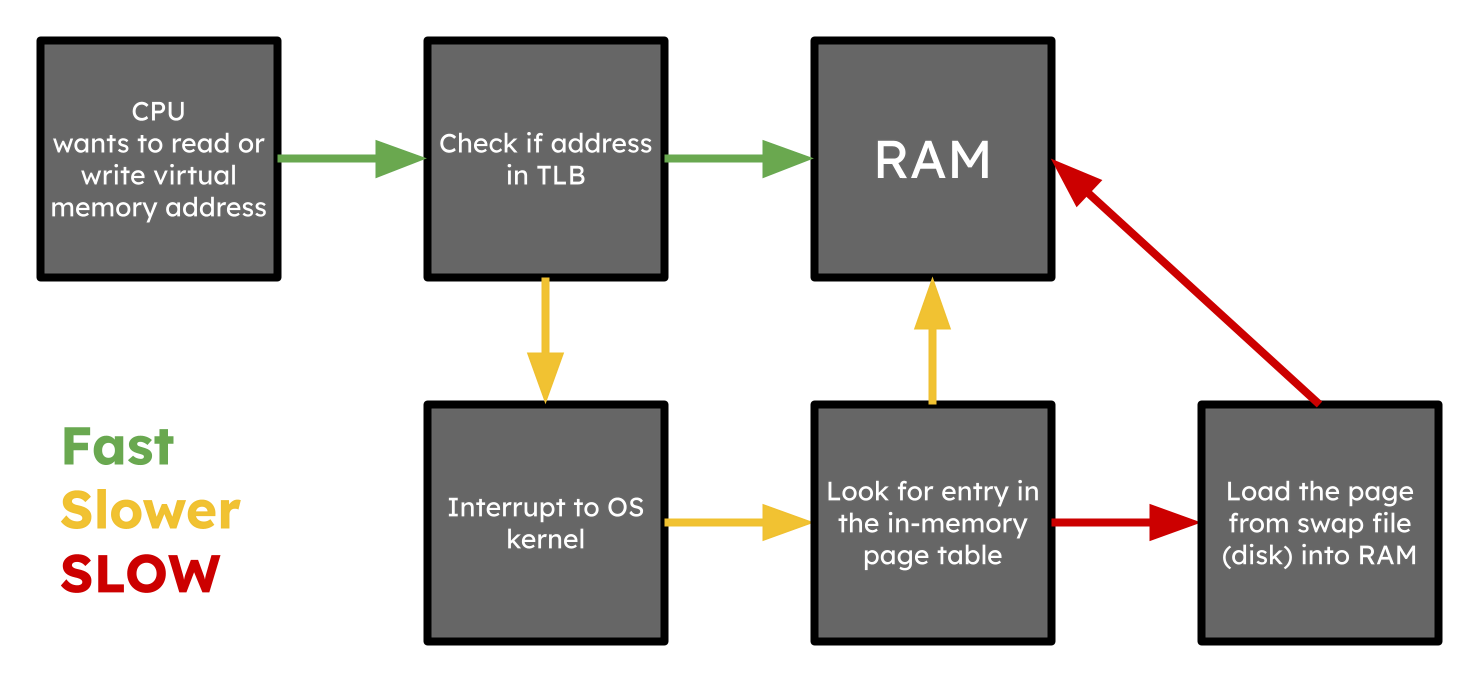
In this simplified scenerio (that ignored CPU memory cache), when a CPU instruction needs to access memory an address, the TLB is checked first. This is a REALLY fast, in-hardware cache for the page table. If the address it needs is present, there is basically zero overhead to doing this memory translation, and it can immediately determine where the virtual address (the address the process thinks it is accessing) maps to in RAM (the actual, physical location of the memory on-chip). Ideally, the vast majority of memory lookups are handled by the TLB, but this depends on the memory access pattern of the program.

If it is not present in this cache, there will likely be an OS interrupt, which then triggers the OS to check if it has an up-to-date mapping for that address in the page table. If it does, then the address is brought into the TLB and the instruction re-executed. This is a bit slower since a RAM lookup is slower than a TLB lookup, but still not too bad.

The REALLY slow case is in the scenario where the address being looked up is valid, but the memory is not in RAM. Programs that use a large amount of RAM can have some of their memory swapped out to be saved on disk. This can happen when the amount of memory being used by a process in its virtual address space is larger than the amount of RAM available. In this case, the memory needs to first be brought in from disk, placed in RAM, page table updated, and then the instruction can be re-executed. THIS. IS. SLOW. And by SLOW, I mean slow relative to the speed of a CPU. Of course, to the human eye, it’s still very fast, especially with a speeds solid state storage. However, if this kind of memory access happens many times during a programs execution, the cost adds up.

(NOTE: I’m skipping over TONS of details here. For more info, check out Wikipedia)

What happens when you malloc?

Precisely what happens when heap memory is allocated via standard library calls such as malloc and calloc is, yet again, system dependent.

But generally, when these functions are used to allocate large segments of memory (such as 1 gigabyte in the code from earlier) the memory is not actually all “loaded” into ram and updated in the page table immediately. Instead, the OS “reserves” space for this memory, but is lazy about allocating it and placing it in RAM until it is written to in the future. The steps for a large malloc are, more or less:

The allocation itself, even if very large, can potentially be a constant-time operation. However, when it comes time to modify this allocated memory, there is extra work to place the memory pages into RAM. What I outlined about is gone over in a bit more detail in this gist. Dive into that for more details.

As we saw, it’s also possible to use more virtual memory that you have physical RAM for. In this case, when there’s no more room in RAM, some of your memory pages can be “swapped out” to be saved on disk. As you can imagine, there is significant overhead each time memory in RAM needs to get saved to disk. If that memory is needed again in the future, it needs to be brought back from disk and placed in RAM, which might evict some other page to the disk. Because the OS kernel has this mechanism, it allows a single computer to use more memory that it has RAM, but this means that performance will degrade when this point is reached due to all of the excess I/O.

Back to C

With this in mind, lets circle back to the two options from before.

// Option A
pagez(80, 1);
// Option B
pagez(20, 4);

(Scroll up to look at the pagez function again if you need to). Recall that option A ran in ~10 seconds and B in ~14. Even though they both have the same exact number of writes to memory pages, the latter is 4 seconds slower. This added slowness is caused by needing more disk I/Os to complete.

Let’s say that each of these programs is allowed to use up to 10 gigabytes of RAM by the OS (my computer has 16, but of course some of it is needed for other things!). When option A executed, it does not need to swap anything out to disk for the first 10 gigabytes of memory needed. After it exhaust all of the RAM the OS is willing to give it, it will need to swap memory out to disk for each page written to in the 80 gigabytes on the heap. However, it should not need to swap any of this 80 gigabytes back in after sending it to swap, as we never visit the same page in this 80 gigabytes of memory more than once. At most, every heap-allocated page is swapped out to disk once.

For option B the first 10 gigabytes is the same story. Then, for the next 10 gigabytes, each memory write will cause a page to get swapped out to memory. However, the program then goes back for three more passes over the same memory. Every page write thereafter will require both a swap out AND a swap in of memory that was previously offloaded. This is what leads to that additional This adds overhead, and explains why the program takes longer!

When a program tries to access memory that is in the page table but not currently mapped to RAM, this is known as a page fault. Both A and B, but especially B, should cause a ton of these, and you can use top to inspect this. Try executing the following:

$ top -stats pid,command,cpu,mem,faults

And then run optionB. Notice how as optionB runs, the number of page faults grows.

For fun, let’s consider one other scenario:

// Option C
pagez(2, 200);

This writes to every page in 2 gigabytes of virtual memory but makes 200 passes. This is way more writing than the other two. And yet:

$ time ./optionC
./optionC  0.37s user 0.13s system 96% cpu 0.516 total

It can go way faster, because as long as my computer has sufficient RAM, scanning over those 2 gigs does not cause any swapping to disk.

Databusses

Since I work for PlanetScale, I’d be remiss if I didn’t somehow squeeze a databases tidbit in here too! When working with databases such as MySQL (and many others) you can encounter similar scenarios, except for database page caches instead.

In MySQL, one of the many configuration options is innodb_buffer_pool_size. If you are using the InnoDB storage engine, this controls how large the page cache will be for keeping pages from your database in memory. If you have indexes and / or a schema that is much larger than the size of the buffer pool, you can end up with lots of puffer pool (cache) misses, leading to pages swapping in and out of this cache, worsening performance.

For example, I have a database named chat containing 100 million rows, totalling 14 gigabytes:

$ du -h /opt/homebrew/var/mysql/chat/*
 14G	/opt/homebrew/var/mysql/chat/message.ibd

And I have my innodb_buffer_pool_size set to only 128 megabytes:

innodb_buffer_pool_size=134217728

I have a python program which makes a connection to this database:

import sys
import math
import random
import os
import MySQLdb

connection = MySQLdb.connect(
    host='127.0.0.1', user='root',
    password='password', db='chat')
cursor = connection.cursor()

And then I’ll run 20 million queries against this DB, in two different variations:

# Variation A
for i in range(1, 100000000, 10):
    for reps in range(0, 2):
        cursor.execute('SELECT alias FROM message WHERE id = %s;', (i,))
        cursor.fetchone()

Here, I select the alias of every row with an ID that is a multiple of 10. For each, I execute the same select query twice in a row before moving on to the next.

# Variation B
for reps in range(0, 2):
    for i in range(1, 100000000, 10):
        cursor.execute('SELECT alias FROM message WHERE id = %s;', (i,))
        cursor.fetchone()

Notice how I swapped the loops in variation B. This one executes the same queries, but in a different order. The alias for rows with IDs that are multiples of 10 are selected in two passes over the rows.

Yet again, which will be slower? Though of course were still dealing with virtual memory issues under-the hood, the issue at hand here is that after the buffer pool / cache fills up, each of these programs will have different numbers of cache hits / misses. Variation A will eventually fill the buffer pool, and then when additional pages are needed it will need to evict / load. However, since queries for the same ID are made in pairs, the second one in each pair should never cause a cache miss. In variation B, after the buffer pool fills, there should be many more misses, likely leading to worse performance. The timing agrees with this.

$ time python3 a.py
python3 generate_load.py  164.50s user 94.81s system 29% cpu 14:29.96 total
$ time python3 b.py
python3 generate_load.py  173.15s user 95.64s system 25% cpu 17:42.87 total

Access pattern

These scenarios, and many more, can all be framed in terms of their memory access pattern. When assessing the performance workloads on large data sets or with big in-memory data structures, taking this into account in your algorithm design can have a significant impact on performance. Looks at from a purely theoretical / big-O perspective is not always sufficient. Now you know. Happy hacking!

Additional references